| 1. The spherical earth | 2. Eratosthenes’ method | 3. Distance | 4. Angle of the sun |
(d) Distance
Distances quoted by Eratosthenes
Eratosthenes’ chosen sites were Meroë, Syene, and Alexandria. He reckoned the straight-line distance between each pair as 5000 stadia.
[T]he meridian through Syene is drawn roughly along the course of the Nile from Meroë to Alexandria, and the distance is about 10,000 stadia. And Syene is situated halfway between them, that is, 5000 stadia from Meroë.
Eratosthenes, Geography fr. 34 Roller (Strabo 2.5.7)
So the distance from Syene to Alexandria must be one fiftieth of a great circle of the earth: and this is 5000 stadia. Therefore, the entire circle works out to be 250,000 stadia. And this is how Eratosthenes’ calculation goes.
Eratosthenes, Measurement M6 Roller (Kleomedes 1.7, 100,19–23 Ziegler)
From Syene to Meroë, Timosthenes the commander of Philadelphos’ fleet gave no measurement but said it was a journey of 60 days; Eratosthenes gave it as 625 [Roman] miles; Artemidoros, 600 miles.
Pliny, Natural history 5.59
| Note. The third passage doesn’t appear in Roller’s edition of the Eratosthenes fragments, for some reason. Pliny’s figure of 625 miles represents 5000 stadia: a Roman mile was 5000 Roman feet. At 2.85 and 12.53 Pliny quotes the rate of 1 stadion = 625 Roman feet = 1/8 of a Roman mile. |
How did he obtain this distance? The most popular answer is based on Martianus Capella, writing in the 5th century CE:
In fact Eratosthenes was informed by Ptolemy’s royal surveyors [mensores regios] about the number of stadia from Syene to Meroë ...Martianus Capella 6.598
At this point we could go on a long tangent. Were these mensores a special category of surveyor known as ‘bematists’? What does that job title entail, exactly? It’d take half an hour. Let’s cut to the chase. Martianus’ mensores weren’t military survey technicians, counting footsteps or wheeling a hodometer through hundreds of kilometres of trackless desert. Or if that is what Martianus imagined, then he’s just wrong.
 |
| Some of the scenery on the direct route between Syene and Meroë. (Base image: Google Earth) |
Eratosthenes used reports published in books that were readily available. And these books described the course of the Nile, not the straight-line desert route between Syene and Meroë.
First, in his Geography he said that he simply repeated the distances he found quoted in these reports, without verifying them.
Eratosthenes states that, for more remote regions, he reports distances that have been handed down, and that he has not verified them but repeated them as he has received them. But sometimes he adds, ‘in a more or less straight line.’Eratosthenes, Geography fr. 131 Roller (Stabo 2.1.41)
Second, we have independent testimony about Greek-speaking writers describing routes and distances between Syene and Meroë. Several Ptolemaic figures travelled to Meroë and beyond, and wrote books about their observations: Dalion, Aristokreon, Bion, Simonides, Philon, Timosthenes, Basilis — and these are just the ones we know about. Pliny tells us that four of these writers explicitly reported distances south of Syene (though he doesn’t report their figures), and that some of them reckoned the total distance from Meroë to the Mediterranean coast as 1250 Roman miles (10,000 stadia).
These people were explorers, admirals, diplomats. They weren’t trundling hodometers along the riverbank, and they certainly weren’t counting paces.
| Note. Pliny, Natural history 6.183. Dalion sailed further up the Nile beyond Meroë and described the wildlife (FGrHist 666). Eratosthenes did not draw on Aristokreon’s account (Aristokreon quoted the distance from Syene to the Mediterranean as 750 Roman miles, i.e. 6000 stadia; FGrHist 667 F 1 = Pliny, NH 5.59). Bion wrote a description of the ethnography and geography of Aithiopia and Nubia (FGrHist 668). Simonides wrote an account of his five years living in Meroë (FGrHist 669). Philon was an agent for the Ptolemaic government who wrote a Voyage into Aithiopia (FGrHist 670). Timosthenes, the naval commander, wrote a substantial account of his voyages (FGrHist 2051) in which he quoted a 60 day travel time up the Nile from Syene to Meroë. |
Put these two points together, and you’ve got Eratosthenes describing the course of the Nile as follows.
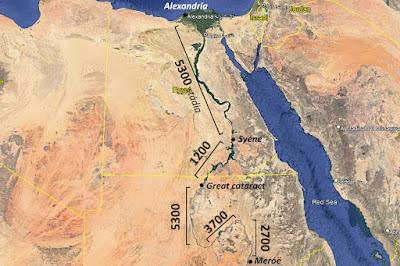
For Eratosthenes says the Nile flows northward from Meroë for 2700 stadia; then it turns back southward, in the direction of the winter sunset, for 3700 stadia; after almost reaching the latitude of Meroë, and projecting a long distance into Libya, it makes its second turn northward for 5300 stadia, until it gets to the great cataract, turning slightly eastward; then 1200 stadia to the smaller cataract at Syene; then 5300 stadia further to the sea.Eratosthenes, Geography fr. 98 Roller (Strabo 17.1.2)
Notice the nice round numbers. They aren’t pure guesswork: these people were experienced professionals, after all. But they weren’t whipping out a theodolite at every bend in the river.
We can only conjecture how Eratosthenes reckoned this meandering route as 5000 stadia in a straight line. In the second stretch, at least, his figures imply a bearing directly southwest. Further north, it isn’t clear where exactly he imagined the river ‘turning slightly eastward’. The 1200 stadia stretch from the great cataract to Syene surely represents the Triakontaschoinos, or ‘land of 30 schoinoi’: this is probably the origin of Pliny’s claim that Eratosthenes reckoned the schoinos as 40 stadia (see below). Here are some speculative reconstructions.
Whatever the details, a lot of approximation was involved. It takes a lot of massaging to make Eratosthenes’ measures look like the real course of the Nile. And we certainly shouldn’t be imagining some poor sap counting footsteps through hundreds of kilometres of desert along the direct route.
Eratosthenes’ distances were travellers’ educated estimates. They weren’t exact measures carefully surveyed with high-precision equipment.
| Note. Priskin 2004 argues that these distances, and the 5300 stadia from Syene to Alexandria in the same passage, are derived from native Egyptian reckonings. The idea is that Eratosthenes drew on a Greek-language report in which distances in Egyptian schoinoi were converted to stadia at the rate of 50 stadia to the schoinos. I used to find this argument compelling, but it doesn’t stack up in light of the 3rd century BCE geographical literature mentioned above. Eratosthenes’ use of Timosthenes is directly attested (FGrHist 2051 T5–T8), and we know his figures had strong similarities to Philon’s (Geography fr. 40 Roller = FGrHist 670 F 2). |
The length of the stadion
So, we’ve got distances of 5000 stadia. What’s that in modern units?
Our evidence for the length of a stadion varies greatly in its character and usefulness. Here’s the executive summary: the stadion as a metrological unit was anywhere between 177 m and 192 m, with the most traditional figure being an eighth of a Roman mile, that is, 183–185 m.
It’s also been suggested that stadia could also act as an itinerary unit when measuring long distances. You can think of this distinction as scientific versus practical. In metrological units, the distance from New York to Los Angeles is 3940 km (2450 miles) as the crow flies. In itinerary units, it’s six or seven days’ drive.
We have three types of evidence for the stadion.
- Physical ancient racetracks, the literal meaning of stadion. These range from 177.3 m (Delphi) to 192.3 m (Olympia).
- Ancient sources report a variety of conversion rates to other reckonings, namely the Roman mile and the Egyptian schoinos.
- Reports of long distance measurements may indicate that the stadion could also be an itinerary measure.
The first two categories are basically metrological. Ancient units aren’t as precise as modern units, but the Roman mile was relatively stable and precise. Modern scholarship has a habit of treating it as 1480 m, thanks to a 19th century study; a more recent study puts it anywhere in the range 1465 to 1481 m. One eighth of that puts the stadion at 183 to 185 m, in good agreement with the racetracks. We do hear of some variations — 7.5 stadia to the mile, or 8.25, or what have you — but nothing too serious.
| Note. Duncan-Jones 1980: 127 reports on evidence for the centuria which implies a Roman foot of 292.92–296.25 mm, and therefore a mile of 1464.60–1481.25 m (1 Roman mile = 5000 Roman feet). The 19th century study is that of Hultsch 1882: 88–90, who reports a range for the foot of 295.5–297.0 mm. The 8 : 1 rate goes back at least to Polybios (2nd cent. BCE; 3.39.8). |
As for the schoinos — that’s the Greek name; the Egyptian word was itrw, literally ‘river’ — modern scholars like to quote a prototypical length of 10.5 km. This figure was devised in the early 1900s from some sample distance measurements, in conjunction with the fact that 10.5 km happens to be a nice round multiple of Egyptian royal cubits: 20,000 royal cubits of 0.525 m = 10.5 km. (There is no documentary basis for the 20,000 cubit figure.)
| Note. For the origin of the 10.5 km and 20,000 cubit figures, see Tupikova 2022: 322–323, citing Loret 1903 and Borchardt 1921. |
Now, here’s what Pliny says about converting between the stadion, the Roman mile, and the schoinos.
By Eratosthenes’ reckoning, a schoinos is 40 stadia, that is 5 miles; some have given a rate of 32 stadia to the schoinos.Pliny, Natural history 12.53
Three things to notice here.
- Pliny repeats the usual 8 : 1 conversion rate for the mile, implying a stadion of 185 m.
- If we instead started from a schoinos at 10.5 km, his figures would imply a mile of 2630 m and a stadion of 263 m or 328 m.
- The 40 : 1 rate probably comes from the distance of 1200 stadia that Eratosthenes quoted for the Triakontaschoinos or ‘land of 30 schoinoi’, from the great cataract northward to Syene.
The key to resolving this apparent inconsistency is that the schoinos was not normally a metrological unit. It was an itinerary unit: specifically, a chunk of a boat journey upriver (recall that itrw means ‘river’). It may have described a stretch of the Nile covered by one towing team (New Pauly s.v. ‘schoinos’).
So you’d expect its physical length would vary depending on terrain. And that’s exactly what ancient sources tell us.
[From Alexandria to the top of the Delta] Artemidoros states that the journey upriver is 28 schoinoi, which is 840 stadia, reckoning 30 stadia to the schoinos. But when I made the trip, they gave the distances using different reckonings in different places, so that they agreed on 40 stadia or even more to the schoinos ... Artemidoros himself [says] ... that from Memphis to the Thebaid the conversion is 120 stadia to the schoinos, and from the Thebaid to Syene it is 60 ...Strabo 17.1.24
Pliny and Strabo make it crystal clear that they’re talking about variations in the length of the schoinos, not the stadion. They’re using stadia to express that variation. Pliny makes similar statements about the Persian schoinos (Natural history 6.125).
Some modern reports are cautious enough about the schoinos to call the 10.5 km figure a convenient ‘average’. Even that’s doing it a kindness.
The upshot is that the schoinos is utterly useless for reconstructing other ancient units.
|
Note. In this series I wanted to tell the true story without distractions, but there’s no dodging some widely repeated falsehoods. The following claims come from Friedrich Hultsch (1882: 60–62), and they are all false. For fuller explanations see Appendix B below.
|
Our useful metrological evidence boils down to the racetracks and the Roman mile. And as we’ve seen, they’re broadly in agreement, if not very precise: they produce a metrological stadion of 177–192 m, or let us say, 185 m ± 8 m.
It remains to consider the possibility of reckoning in itinerary stadia. A useful 2022 article by Irina Tupikova goes over this, looking at ancient sources generally, not just Eratosthenes.
Where distances quoted by ancient sources can be compared with the real distances, her analysis indicates that distances under 1000 stadia (in metrological terms, 185 km = 115 miles) tend to be significantly overstated. Distances over 1000 stadia are very variable, sometimes overstated, sometimes understated.
You can explain this in two basic ways:
- Ancient surveying methods weren’t very accurate.
- Distances between cities are a representation of journey times.
Take a modern analogy. Let’s say you’re aware that it’s six or seven days’ drive from New York to Los Angeles. If you accept a common reckoning that you can drive 800 km (500 miles) in a day, you can estimate the total distance as 4800–5600 km (3000–3500 miles). The real distance by road is 4500 km (2800 miles). (Why the discrepancy? All sorts of reasons: fatigue, terrain, supplies, accidents, etc.)
So we could say that the distance is 4800–5600 km in ‘itinerary kilometres’, which are about 7%–17% shorter than actual kilometres. I’m not saying this would be wise. But you could.
This is the kind of conclusion Tupikova reaches about stadia. For land distances over 125 Roman miles, Pliny the Elder reports distances which could be taken to suggest an ‘itinerary mile’ which is shorter than the 1480 m mile by 7% to 23%; for sea distances under 125 miles, his miles tend to be around 36% short. When Strabo reports distances from Eratosthenes’ Geography, they could represent an itinerary stadion around 13% to 31% short of the 185 m stadion.
If you take the ‘itinerary stadion’ at face value, Eratosthenes’ measurement turns out to be highly accurate. Tupikova reckons that the measure of 157.5 m represents Eratosthenes’ ‘itinerary stadion’: using that, his measurement of the earth’s circumference at 252,000 stadia is impressively precise: it comes to 30,690 km, just 0.79% shy of the true value.
Except that’s total nonsense. It’s circular. The argument goes: if we use distance units based on the figures that Eratosthenes gives for the distances between Alexandria–Syene–Meroë, then his measurement of the earth, which is also based on those same figures, turns out to be accurate too.
When you put it that way, the 0.79% precision isn’t quite so amazing.
That isn’t what the ‘itinerary kilometre’ and the ‘itinerary stadion’ are for. They don’t work like that. If someone travelling across America converted ‘six days’ drive’ to kilometres at the rate of 800 : 1, and you confronted them with the true metrological distance, they wouldn’t say: ‘Well actually I was working in itinerary kilometres, and in those, my measurement is perfectly precise.’ No: they’d admit that it was an estimate.
Eratosthenes would say the same. In fact he did say the same. Remember, he openly stated that he didn’t verify his figures.
Eratosthenes didn’t quote the distance from Syene to Meroë as 5000 stadia because he was using ‘Eratosthenean stadia’, and Eratosthenean stadia happen to be 1/5000 of that distance. He did so because he relied on imprecise measurements.
The circumference of the earth
We’re left with the metrological stadion, of 177–192 m. Using that standard, Eratosthenes’ figure of 5000 stadia for the distances Alexandria–Syene and Syene–Meroë is too high. 5000 stadia is between 890 and 960 km; the real distances, as the crow flies, are 840 km and 800 km respectively; the north-south separation, ignoring the different longitudes, is 790 km for both distances.
That puts Eratosthenes’ figure for the earth’s circumference between 44,680 km (stadia of 177.3 m) and 48,460 km (stadia of 192.3 m). The traditional reckoning of 8 stadia = 1 Roman mile (1480 m) gives 46,620 km. The earth’s true polar circumference is 40,008 km. Eratosthenes’ result is between 11.7% and 21.1% too high; the traditional reckoning is 16.5% high.
There’s no need to make excuses for that. This is still impressive for the 3rd century BCE. It doesn’t need to be accurate within 0.79% to be a terrific achievement. And it has to be said, given that Eratosthenes didn’t verify his data, he got lucky. The estimates he used could easily have been much wilder.
Next week, the finale: part 4, the problem of measuring the sun’s angle.
Appendix A. Table of ancient sources
Here I give the lengths of physical racetracks and ancient conversion rates between the stadion, schoinos, and Roman mile, treating them as if all three were metrological units.
| Source | Conversion rate | Resulting length of stadion |
|---|---|---|
| Ancient racetracks (Gulbekian 1987: 360; New Pauly s.v. ‘stadion’) | — | 177.3–177.5 m (Delphi) 181.3 m (Epidauros) 184.3–185.0 m (Athens) 191.4 m (Miletos) 192.25–192.30 m (Olympia) |
| Herodotos 2.6, 2.9 | 60 stadia = 1 Egyptian schoinos | 175.0 m (schoinos = 10.5 km) |
| Herodotos 2.149; pap. Heidelberg 1289 | 1 stadion = 400 Egyptian cubits | 210.0 m (royal cubit = 0.525 m) |
| Eratosthenes, reported by Pliny, Natural history 12.53 | 40 stadia = 1 schoinos | 262.5 m (schoinos = 10.5 km) |
| ‘others’, reported by Pliny, Natural history 12.53 | 32 stadia = 1 schoinos | 328.1 m |
| Artemidoros, reported by Strabo 17.1.24 | 30, 60, or 120 stadia = 1 schoinos | 350.0 m, 175.0 m, or 87.5 m |
| Strabo 17.1.24 | 30 or 40 stadia = 1 schoinos | 350.0 m or 262.5 m |
| Geometrika (pseudo-Heron) ii.6, iii.5 Bruins | 30 stadia = 1 schoinos 45 stadia = 1 ‘barbarian’ schoinos 60 stadia = 1 ‘Persian’ schoinos |
(these illustrate that the schoinos is an itinerary measure, not metrological; also claims that the Roman mile = 5400 Roman feet) |
| Eratosthenes, reported by Pliny, Natural history 5.59, 2.85, 12.53 | 40 stadia = 5 Roman miles; Syene to Meroë (5000 stadia) = 625 Roman miles | 185 m (mile = 1480 m) |
| Eratosthenes and Strabo, reported by Julian of Ascalon (i.201 Hultsch) | 8¼ stadia = 1 mile | 179.4 m (mile = 1480 m) |
| Polybios 3.39.8 | 8 stadia = 1 Roman mile | 185 m (mile = 1480 m) |
| Polybios, reported by Strabo 7.7.4 | 8⅓ stadia = 1 Roman mile | 177.6 m (mile = 1480 m) |
| ‘most people’, according to Strabo 7.7.4 | 8 stadia = 1 Roman mile | 185 m (mile = 1480 m) |
| Plutarch, Gaius Gracchus 7.2 | a little under 8 stadia = 1 Roman mile | a little over 185 m (mile = 1480 m) |
| Censorinus 13.2 | 1 stadion = 625 Roman feet (⅛ mile) | 185 m (mile = 1480 m) |
| Dio Cassius 38.17.7, 39.50.2, 46.44.4, etc. | 7½ stadia = 1 Roman mile | 196.1 m (assuming post-200 CE mile ≈ 1471 m: Hultsch 1882: 97) |
| Julian of Ascalon i.201 Hultsch | 7½ stadia = 1 Roman mile | 196.1 m (post-200 CE mile ≈ 1471 m) |
| Geometrika 22.1 Heiberg | 7½ stadia = 1 mile = 4500 royal feet = 5400 ‘Italian’ feet | (meaning obscure; the ancient Roman mile = 5000 Roman feet) |
Appendix B. Problems with Hultsch’s account of ‘Eratosthenes’ stadion’
- If the schoinos really were ‘firmly determined’, then the ‘average’ schoinos of 10.5 km would mean (a) at the 40 : 1 and 32 : 1 rates that Pliny quotes, the stadion was 263 m or 328 m; (b) Artemidoros’ reckoning would produce a stadion anywhere from 88 m to 350 m. Hultsch’s reckoning of 157.5 m doesn’t fit in here anywhere.
- All scholars in the last century have quoted a rate of 20,000 cubits in the ‘average’ schoinos, not 12,000 (see e.g. Priskin 2004; Tupikova 2022: 323). As we’ve seen, (a) even that’s just a byproduct of the 10.5 km reckoning, and (b) it’s far too precise, given that the schoinos is itinerary while the cubit is metrological.
- The only basis for the 12,000 cubit figure is the pseudo-Heronic Geometrika, which comes with its own problems.
- It’s idiosyncratic: e.g. it quotes the rates 1 ‘mile’ = 5400 ‘Italian’ feet = 4500 phileteric feet, rather than the 5000 foot standard.
- The Geometrika gives a rate of 30 stadia to the schoinos.
- The Geometrika treats all these units as metrological: this wasn’t the case in antiquity.
- The vocabulary of the Geometrika implies a Byzantine date. It refers to ‘Italian’ feet and miles rather than ‘Roman’, surely on the grounds that by the time it was written, ‘Roman’ included all of the units it lists. It was only around the 5th century CE that ‘Roman’ started to be used for the people of the eastern empire. The Geometrika should be grouped with Julian of Ascalon among sources too late to be relevant.
- Hultsch selectively disregards the 8 : 1 rate with the mile which Pliny attributes to Eratosthenes in the same sentence; the 8¼ : 1 rate with the mile which Julian of Ascalon attributes to Eratosthenes; the 30 : 1 rate with the schoinos in the Geometrika; and all of Polybios’, Artemidoros’, Strabo’s, and Plutarch’s testimony (among others).
- These selections are transparently aimed at trying to make Eratosthenes’ measurement work out to be as accurate as possible.
- The only basis for the notion of ‘pacing out distances’ is the etymology of the rare word βηματίζω ‘measure’. The primary meaning comes from the distance unit the βῆμα (‘pace’, usually 2.5 or 3 feet). Ultimately both are derived from βη- ‘walk’, but etymology isn’t a reliable guide to meaning. Prior to the Byzantine period βηματίζω appears only in contexts where literal measurement by pacing would be impossible (Dionysios Chalkous fr. 3.5 West) or where we know other measuring methods were used (Polybios 3.39.8).
- Although Hultsch’s account has long been rejected, much of his misinformation lingers. Popular accounts still accept without question that the stadion and the schoinos were 157.5 m and 12,000 cubits. Even Tupikova’s 2022 article gives airtime to the 157.5 m stadion, and the notion of surveyors pacing out distances.